Copyright © Karl Dahlke, 2022
Science, or at least the quest for science, began in Greece around 400 B.C. This is one of those statements that is too simple to be entirely true, yet I believe it contains a core of truth nonetheless.
Certainly the Greeks cannot claim to be the fountainhead of math and engineering. Egypt built most of its pyramids nearly 2,000 years earlier, a staggering accomplishment that would be difficult to replicate today, even with modern machinery. How much math did that entail‽ They developed simple machines, pulleys, rollers, levers, capable of multiplying human strength 100 fold - centuries before Archimedes described the 6 simple machines. Still, Archimedes was able to characterize those machines, describe how they work, and calculate mechanical advantage. If you use a wheel and axel, your strength is multiplied by the ratio of the two diameters, while distance is cut by the same ratio. He didn't realize it, but he was laying the foundation for the "conservation of work", which would later become the "conservation of energy", a mighty scientific principle. Referring to the power of the lever, he famously said, “Give me a place to stand, and I shall move the world.” He knew that mechanical advantage was unlimited, at least in theory. The Egyptians used simple machines to solve an engineering problem, but Archimedes explained how they work, and how to improve them.
In the same way, the Greeks wanted to go beyond functional arithmetic, and study abstract mathematics for its own sake. The math department at a university is often divided into two halves, applied math and pure math. Prior to the Greeks, all math was applied. What do we need to know to build this pyramid, these walls, this temple? In contrast, Euclid wanted to do something else. His famous book, The Elements, is a compendium of all the pure math that was known at the time, including some of his own original work. He was fascinated with prime numbers, even though they had no practical application. They were beautiful - that's all. He knew, intuitively, that every number is uniquely a product of primes, 21 is 3 times 7 and nothing else, but it would take the genius of Gauss, 2000 years later, to prove it. His theorems on geometry were equally abstract. Some of his results were helpful in construction, but most of his theorems, e.g. deducing all of geometry from 5 postulates, was pure math, and still is today.
Turning to astronomy and physics, the Greeks wanted to understand the world, simply to sate their curiosity. Why do the planets move in the sky, and can we trace their orbits? Why are the tides connected to the phases of the moon? What is matter made of? Is it really earth, wind, water, and fire? These questions aren't related to survival, but the Greeks were curious, so they tried to answer them as best they could, with almost nothing but intuition to guide them. They also took the time to write down their thoughts and ideas. Another civilization might have wrestled with the same questions,but since they didn't leave a written record, we'll never know.
Along with abstract math and basic science, the Greeks developed literature, music, theater, and even new forms of government. Athens is sometimes called the cradle of democracy. No wonder we site the Greek philosophers again and again whenever we discuss the birth of western civilization. This was illustrated on The Big Bang Theory, when Sheldon wanted to teach Penny physics. “it was a warm summers evening in ancient greece.” he began. In many cases, I too will site the Greek philosophers. They were often wrong, but they were on the right track. They didn't know the answers, but at least they asked the questions. Today we understand the world in unprecedented detail, partly because we stand on their shoulders.
A scientist is curious as he searches for the truth, but he is also elated when he finds it. The Greeks were no exception in this regard. When Archimedes discovered the concept of displacement, he jumped out of his bath and ran naked through the streets, shouting, “Eureka!”, as he could not contain his joy. I dare say, scientists and mathematicians feel the same way today, though there are laws against indecent exposure, so we have to be careful.
Sometimes this joy is contagious. When Pythagoras proved the theorem that bears his name, the Pythagorean theorem, the proof was so beautiful and elegant, that he celebrated by sacrificing several oxen, providing a feast for the entire town. (This story may be apocryphal, but I hope it is true, and I wouldn't be surprised if it was.) The Pythagorean theorem was known for thousands of years by observation, i.e. engineers knew how to derive the third side of a right triangle from the other two sides, but they didn't have a proof. Nobody knew why it was true, until Pythagoras solved the thousand year old math conundrum, using an argument so compelling that it could not be denied. Not all proofs are beautiful, but this one is. He must have shouted “Eureka”, as he showed his drawings to passers by. I would like to present the proof below, and perhaps you will feel like celebrating as well. This is not related to anything else in the book, so you can skip ahead to the next chapter if you like, but I hope you will follow along, it's really quite lovely.
Suppose you want to tile a floor that is 5 feet by 7 feet. Each tile is a square 12 inches on a side, that is, one foot square. How many tiles do you need? Answer: 5×7 = 35 tiles. The floor is 35 square feet in area and each tile covers one square foot so you need 35 tiles.
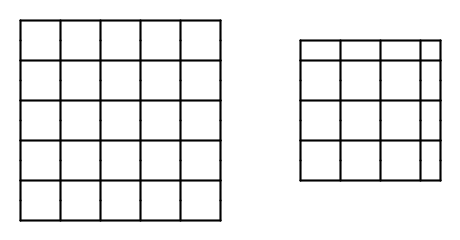
If the floor itself is a square, say 8 feet by 8 feet, then you need 8×8 = 64 tiles. This is called 8 squared, shorthand for 8 times 8, and it is written 82. It's just notation for multiplying a number by itself. It works for integers, but it also works for fractions and decimals. The left image is a standard 5 by 5 tiling; the right image is a square region that is 3.5 units on a side. The area is 3.5 squared, or 3.5 times 3.5, which is 12.25 - and it actually works. The region contains 9 complete tiles, 3 half tiles on the right, 3 half tiles on the top, and a quarter tile at the upper right, which adds up to 12 and a quarter.

Turning to variables, the area of a square that is a units on a side is a2, and the area of a square that is b units on a side is b2. The area of a rectangle that is a by b is a times b, or a×b, or ab for short. In algebra, numbers and variables that stand next to each other are multiplied together.
With squares and rectangles under control, what is the area of a right triangle that has a base b and a height of a? Two such triangles fit together to make a rectangle, as shown below, thus the area of a single triangle is half of a×b, or half of ab, or ½ab, or ab/2.
| a |

|
| b |
Let a right triangle have base b and height a, and let the hypotenuse, the long slanted side, have length c. The pythagorean theorem relates the lengths of the three sides as follows.
a2 + b2 = c2
As mentioned earlier, this was known for some time. If a slanted beam provides structural support from the floor on one side to the ceiling on the other, the length of that beam can be determined. Engineers knew in advance how long the beam should be, so they cut it accordingly and fit it into place. Yet nobody knew why this was true, nobody could prove the relationship, until Pythagoras. Before I present the proof, let's test the theorem in practice.
Cut a right triangle out of paper or cardboard, having legs 3 inches and 4 inches. You can literally measure and cut the corner off of a piece of cardboard, thus guaranteeing a right angle. Now measure the hypotenuse. It should be exactly 5 inches. This because 32 + 42 = 52, that is, 9 + 16 = 25.
Cut a right triangle out of paper or cardboard, having legs 12 inches and 5 inches. (You can use centimeters, or any other units you like.) Now measure the hypotenuse. It should be exactly 13 inches. This because 122 + 52 = 132, that is, 144 + 25 = 169.
Cut a right triangle out of paper or cardboard, having legs 6 inches and 5 inches. Now measure the hypotenuse. It should be approximately 7.81 inches, since 7.81 squared is nearly 61. (Try it on a calculator.) The hypotenuse doesn't have to come out exact, and it usually doesn't. It is usually a decimal number. Take the square root of 61 on a calculator for more digits.
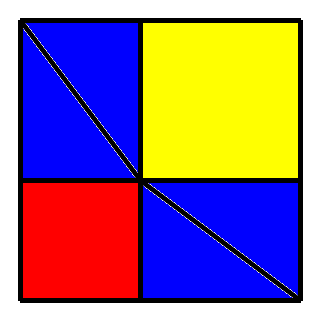
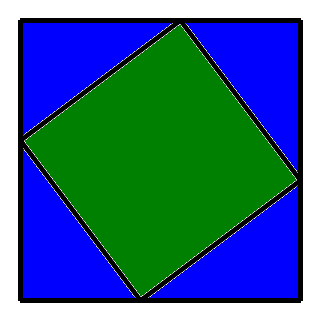
Seeing all those squared terms, Pythagoras knew it had something to do with area. This is not clear at the outset, since a b and c represent the lengths of the three sides. So the area of what? It took a flash of genius to find the answer. Pythagoras drew a square, a+b on a side, and measured area in two different ways. Note that 4 triangles are placed strategically in the square. He measured the area of the square, without the triangles, which must be constant, no matter how you arrange the triangles. Each triangle has legs a and b, and a slant of c. The area with the triangles omitted is either a2 + b2, or c2. And that completes the proof.
|
|
Honestly - isn't that absolutely beautiful‽ If you were the first person on earth to come up with that, you'd feel like celebrating too.
When the Wizard gives the Scarecrow his diploma, in lieu of a brain, the Scarecrow misquotes the theorem: “The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side.” Nonsense! Perhaps the writers did this deliberately; after all, the Wizard was a sham, and didn't have the power to give the Scarecrow an actual brain.